温度計に関する一口メモ
【絶対温度】
【ウィーンの変位則】
熱力学から生まれ、物質の特異性に依存しない温度目盛を定義したものです。
1848年、ケルビンによって導入され、0℃=273.15Kと定義されています。対温度Tと放射される赤外線のピーク波長(λmax)が反比例することを表わす公式です。
λmax・T=a(一定)
λmax:ピーク波長
a:ウィーンの変位定数2897.8μm・K
【熱平衡】ねつへいこう
【キルヒホッフの法則】
温度差のあるふたつの物体を接触させると、物体の熱が熱い方から冷たい方へ移動し、やがて一定となります。
この状態を熱平衡といいます。一般の接触型温度計はこの原理を利用しています。
また、接触型温度計で熱容量の小さな物体を測定する時、温度計の影響によって測定物体の熱平衡状態が乱れ、温度が変化してしまう現象を 【熱じょう乱】といいます。物体固有の赤外線放射率は、その物体の吸収率に等しいことを表わした法則です。
熱平衡状態においては、放射される赤外線と吸収される赤外線の量は一致します。
例えば下図のように熱平衡状態(同じ温度)の物体aとbがあります。aから放射される赤外線の一部が、bによって反射あるいは吸収されるものと仮定すれば、吸収されることによってbの温度が上昇することになります。
ところが、aとbは熱平衡状態ですからbだけの温度が上昇するのは不自然なことになります。
つまり、吸収した量と同じ量の赤外線をbが放出していると考えればいいわけです。この法則を確立したのがキルヒホッフです。
【ステファン・ボルツマンの法則】
絶対温度と全放射エネルギーの関係は、プランクの放射法則を全波長で積分したもので、絶対温度の4乗に比例します。
E=σT4
E:全放射エネルギーW/m2
σ:ステファン・ボルツマン定数
5.6697×10-8 W/m2 /K4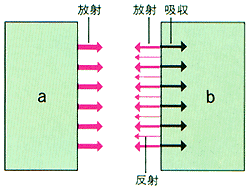
【波長の単位】
【プランクの放射法則】
波長の場合、通常λ(ラムダ)という記号が用いられ、単位としてμm(ミクロンメータ)またはnm(ナノメータ)が使われます。また、分子構造などに関係する赤外線の単位はcm-1(カイザー)が使われています。
1cm =10-2 m 1mm =10-3 m
1μm =10-6 m (0.000001m)
1μm =1000nm=10-3mm=10-4 cm
1nm =10-9 m (0.000000001m)
1nm =10-3 μm=10-6 mm=10-7 cm
1A(オングストローム)=10-10m(0.0000000001m)
1A(オングストローム)=10-4μm=10-8 cm
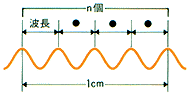
cm-1(カイザー)=波の個数/1cm
(1cmの中に入っている波の数)
例えば波長(λ)が1μmの場合、
1μm=10-6 m=10-4 cm
カイザーに変換すると1/10-4 cm=104 cm-1になります。
したがって、1μmの場合、1cmの中に1万個の波が存在していることになります。温度と波長によって求められる、黒体が半球空間に放射する熱放射エネルギーの公式です。
E(λ・T)= C1/λ5・1/exp(C2/λT)-1
E(λ・T:放射エネルギー密度W・μm/m2
λ:波長μm
T:絶対温度K
C1:プランクの放射第一定数3.7415×108 W・μm4 /m2
C2:プランクの放射第二定数1.43879 μm・K
【センサー】
赤外線センサーは大きく分けて「熱型」と「量子型」に分類できます。
熱型センサーは、赤外線を受けることにより温度が上昇します。
この温度上昇によって起こる焦電現象、熱起電力の変化などの電気的性質を電気信号に変換します。
この熱型センサーには、焦電素子、サーモパイルなどがあります。
また、量子型センサーは、赤外線を受けるとセンサーが直接励起され、電力的な性質に変化を生じます。
この変化量を電気信号に変換します。この量子型センサーには、シリコンセンサー、ゲルマニウムセンサーなどがあります。
【リニアライザー】
【温度ドリフト】
直線的な比例関係であればすぐに値が求められますが、温度と放射赤外線の関係のように、複雑に変化するものは直線的な比例関係では簡単に求められません。
このようなときに比例関係に置き換えるメカニズムで、放射温度計に内蔵されているROMなどにプログラムされています。測定周囲(放射温度計周辺)の温度が変化することによって測定値が変化することをいいます。
通常、周囲の温度が1℃変化した時に指示値がどの程度変化するかを示す%K/℃や、%/℃の単位で表わします。この数値が小さいほど性能が優れています。
たとえば、温度ドリフトが±0.1%/℃の放射温度計で200℃の測定物体(放射率≒1)を測定している時に、周囲温度が30℃から10℃に変わったとすると
(200℃)×(±0.1%)×(30℃-10℃)=±4℃
となります。
したがって、この場合、196℃~204℃の範囲内におさまります。
【熱伝導率】
【応答時間】
熱の伝わりやすさをいいます。
例えば、接触型温度計でゴム、プラスチックなどの、熱伝導率の小さな測定物体を測定しようとすると、
接触状態にあってもその熱が温度計に伝わりにくく、長い時間を要します。測定物体がステップ的に温度変化したとき、放射温度計がその温度を表示するまでの時間をいいます。
【分光放射輝度】
【精度定格】
各波長点での放射エネルギーの単位面積、単位立体角あたりの強度を表わしたものです。
測定物体の絶対値(真の値)に対する側定値のズレ量で、この値が小さいほど性能が優れています。
【黒体炉】
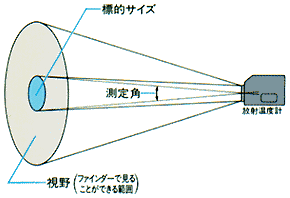
【標的サイズ】
- 放射率がほとんど1に近い値を持つ炉で、放射温度計の校正を行なう時などに使われます。
- 放射温度計が測定している部分の大きさで、通常、ファインダーで確認できます。
【再現性】
【華氏、摂氏のいわれ】
同一条件(測定方法、測定物体など)で繰り返し測定した場合の測定値のバラツキの程度をいいます。この値が小さいほど性能が優れています。
華氏は、ファーレンハイトを中国語で「華倫海」、摂氏は、セルシウスの「攝爾修」(“攝”は“摂”の旧字体)、それぞれの頭文字をとった略号ですが、現在は、カ氏(F)またはセ氏(℃)と略称しています。
【℃/Fの換算式】
【宇宙の温度は-270℃】
℃=5/9(F-32)です。
100Fの温度を℃に換算する場合、
℃=5/9(100-32)≒37.8
100Fは約37.8℃であることがわかります。1965年、アメリカのペンジャスとウィルソンは宇宙のあらゆる方向から来るマイクロ波(宇宙背景放射)をキャッチ。
その強度が、3Kであることを発見しました。
【世界の最低気温は-89.2℃】
【人工衛星から、原発事故を発見】
1983年、南極で記録されました。一方、最高気温は1921年、イラクで58.8℃を記録しました。
(「気象年鑑」1986年版より)「ソ連の原発事故を真っ先に写したのが、人工衛星だった」というのは有名な話です。
これは可視光線から赤外線までさまざまな光をとらえコンピュータ処理された画像でした。
【0.2℃の温度差をキャッチするハブのセンサー】
ハブの鼻孔の脇についているピット器官は、赤外線をキャッチする優秀なセンサーになっています。
この特殊な感覚器官が、獲物を探知し捕獲するのに大いに役立っているのです。